Operator spreading#
Overview#
In this tutorial, we will introduce the operator spreading that serves as a diagnostic of the chaotic dynamics and information scrambling. We will examine operator spreading as a function of the circuit depth \(L\) that can be regarded as the time \(t\) in discrete quantum systems. The operator spreading coefficient considered here reads:
where \(\sigma_{y}^{(j)}\) is the Pauli-y matrix at the \(j\)-th qubit. \(O(0)\) is the Pauli-x matrix located at \(N/2\), i.e. \(\sigma_{x}^{(N/2)}\). And \(O(t)=U(t)^{\dagger}O(0)U(t)\), where \(U(t)\) is the unitary matrix of the circuit with \(t\) layers.
A physical picture for the operator spreading is that if the Heisenberg operator growth \(O(t)\) does not reach the site \(j\), \([O(t), \sigma_{y}^{(j)}]=0\), while the equality will break down when sites \(N/2, j\) become correlated inside the causal region.
Setup#
[1]:
import numpy as np
import tensorflow as tf
import tensorcircuit as tc
import matplotlib.pyplot as plt
tc.set_backend("tensorflow")
tc.set_dtype("complex128")
dtype = np.complex128
Parameters#
[2]:
N = 6 # The number of qubits
L = 2 # The number of circuit layers
num_trial = 1 # The number of random circuit instances
The Unitary Matrix \(U(t)\) of the Quantum Circuit#
The circuit architecture is shown below, each block includes two Pauli rotation gates along the y-axis (\(R_{y}\)) followed by the \(CZ\) gate. We can get the unitary matrix \(U(t)\) of the circuit by setting the input state as an identity matrix.
[3]:
@tf.function()
def get_unitary_of_circuit(v):
layers = len(v)
c = tc.Circuit(
N, inputs=np.eye(2**N, dtype=dtype)
) # when we choose inputs=np.eye(2**N,...), the output wavefunction
# is the unitary matrix U(t) of the quantum circuit
# Ry+Cz
for layer in range(layers):
if layer % 2 == 0:
for i in range(0, N, 2):
c.ry(i, theta=v[layer, i])
c.ry(i + 1, theta=v[layer, i + 1])
c.cz(i, i + 1)
else:
for i in range(1, N, 2):
c.ry(i, theta=v[layer, i])
c.ry((i + 1) % N, theta=v[layer, (i + 1) % N])
c.cz(i, (i + 1) % N)
U = c.wavefunction() # the output of wavefunction is a vector with dim=2^(2N)
U = tf.reshape(U, [2**N, 2**N]) # reshape vector to matrix
return U
Operator at \(t=0\)#
[4]:
# j means the operator locates at the j-th qubit
# a means the type of operator, a=1 (2,3) is the Pauli-x (y,z) matrix
def get_operator(j, a):
I = tc.gates._i_matrix
if a == 1:
σ = tc.gates._x_matrix # Pauli-x matrix
elif a == 2:
σ = tc.gates._y_matrix # Pauli-y matrix
elif a == 3:
σ = tc.gates._z_matrix # Pauli-z matrix
h = []
for i in range(N):
if i == j:
h.append(σ)
else:
h.append(I)
# Pauli-a matrix locates at j-th qubit
operator = h[0]
for i in range(N - 1):
operator = np.kron(operator, h[i + 1])
return tf.cast(operator, dtype=dtype)
Operator Spreading#
The operator spreading \(C_{y}(j,t)=\frac{1}{2} \text{Tr}([O(t), \sigma^{(j)}_{y}]^{\dagger}[O(t),\sigma^{(j)}_{y}])\) can be written as:
[5]:
@tf.function()
def get_spreading(v, σ_y):
U = get_unitary_of_circuit(v)
U_dagger = tf.transpose(U, conjugate=True)
σ_x = get_operator(int(N / 2), 1) # O(0)
σ_x_t = U_dagger @ σ_x @ U # O(t)
σ_x_t_dagger = tf.transpose(σ_x_t, conjugate=True)
C = tf.linalg.trace(σ_y @ σ_x_t_dagger @ σ_y @ σ_x_t)
C = 1 - tf.math.real(C) / (2**N)
return C
[6]:
def main(layers=1):
# use vmap to get operator spreading coefficients of different random circuit instances
# num_trial: the number of random circuit instances
# layers: the number of circuit layers
get_spreading_vmap = tc.backend.vmap(get_spreading, vectorized_argnums=0)
C = get_spreading_vmap(
tf.random.uniform(
[num_trial, layers, N], minval=0.0, maxval=2 * np.pi, dtype=tf.float64
),
[[get_operator(j, 2) for j in range(N)] for _ in range(num_trial)],
)
return tf.reduce_mean(C, 0)[0] # averaged over different random circuit instances
[7]:
C = main(L) # operator spreading averaged over different random circuit instances
plt.bar([i for i in range(N)], C)
plt.xticks(fontsize=16)
plt.yticks(fontsize=16)
plt.ylabel("Operator spreading", fontsize=16)
[7]:
Text(0, 0.5, 'Operator spreading')
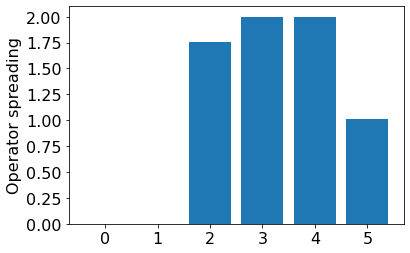
Results#
The operator spreading for a system of \(n = 6\) qubits as a function of \(1 ≤ j ≤ n = 6\) for a different number of layers \(L\), averaged over 20 random circuit instances. When \(L=2\), the Heisenberg operator growth of \(O(t)\) does not reach the site \(0,1\), \(C=0\); when \(L=10\), the equality will break down.