第二章量子力学 (Quantum Mechanics)#

1. 量子力学基础#

量子计算顾名思义，是使用量子力学规律进行计算的全新范式。目前理论和实验已经揭示，量子计算在计算能力上有远远超过传统计算机（也称经典计算）的潜力。量子力学是描述微观物理的最精确的理论，迄今为止得到了海量实验的验证。从数学上来说，量子力学的本质是希尔伯特空间（Hilbert space）及作用于其上的算子。当空间维数有限的情况下等价于在复数域上的线性空间。在本节中，我们将考虑有限维的线性空间及量子计算的基础。相关线性代数的基础知识在附录中给出以供参考。

量子力学的基本原理是一组数学公理，我们先介绍这些公理。

1.1 公设1：希尔伯特空间（Hilbert space）#

任意封闭物理系统都具有一个相关联的具有內积结构的复向量空间（希尔伯特空间），称为量子态空间 \(\mathcal{H}\) 。整个系统的物理性质完全由此空间中的向量来描述，称为态向量 \(\vert\psi\rangle\) 。

说明：

在量子力学中，通常使用狄拉克符号（Dirac notation） \(|\cdot \rangle\) 来表示希尔伯特空间\(\mathcal{H}\)中的向量，读作“ket”。
数学上，我们可以用一个复向量簇（Ray）来表示量子态。这里，\(|\psi\rangle\) 所在的向量簇指代任意向量\(|\psi'\rangle = C|\psi\rangle, C\in \mathbb{C}, C\neq 0\)，这些向量在物理上都是等价的。量子态代表物理系统的一种状态，例如具有某个特定的能量，动量，角动量等。我们可能听说过量子力学的叠加性原理（例如著名的薛定谔的猫）。具体来说，对任意两个量子态\(|u\rangle,|v\rangle \in \mathcal{H}\), \(|u\rangle + |v\rangle \in \mathcal{H}\)，即系统可以“同时”处于多种状态。在我们关心的量子计算领域，\(\mathcal{H}\)维数是有限的(设为\(N\))，那么我们可以选取一组线性无关的向量\(\{|\phi_i\rangle\}=\{|\phi_i\rangle|i=0,\cdots,N-1\}\)作为基向量（basis，例如日常的三维空间在\(x\),\(y\),\(z\)方向的三个单位向量\(\{e_x, e_y,e_z\}\)即为一组基向量）。\(\mathcal{H}\)中的任意量子态都可以用这组基线性展开：

\[|\psi\rangle = \sum_i c_i |\phi_i\rangle, \quad c_i \in \mathbb{C}，\forall i\]

这组基向量也称为完备基。方便起见，在这组基向量下，我们可以将\(|\psi\rangle\)表示成：

\[|\psi \rangle \cong (c_0, c_2,\cdots, c_{N-1})^T, \quad\]

称为\(|\psi\rangle\)在\(\{|\phi\rangle\}_i\)下的表示。这里的展开系数\(c_i\)称为几率幅，\(T\)代表向量和矩阵的转置。这就是我们所熟悉\(n\)维复数向量（列向量）。

正如在欧几里得空间可以定义向量內积一样，我们也可以定义希尔伯特空间的向量內积。我们可以定义\(|v\rangle\) 的对偶向量 \(\langle v|\)（\(\langle\cdot|\) 称为“bra”)。这样我们就有

\[|v\rangle \cong (v_0, \cdots, v_{N-1})^T, \quad \langle v| \cong (v_0^*, \cdots, v_{N-1}^*)。\]

使用Dirac notation方便的原因之一是我们可以将内积表示为“braket”:

\[\langle v|w\rangle = \sum_{i,j=0}^{N-1} v_i^* w_j \langle\phi_i|\phi_j \rangle。\]

可以看出，內积是一种线性算运算，且满足\(\langle u|v\rangle=\langle v|u\rangle^*\)和\(\langle v|v \rangle\geq 0\)。有了內积的概念，我们就可以定义向量的长度：\(\|v \|_2 = \sqrt{\sum_{i=0}^{N-1} |v_i|^2} = \sqrt{\langle v|v\rangle}\)。我们称长度为1的向量为单位长度向量。在接下来的讨论中，我们默认描述系统的量子态的长度为1。至此，我们对\(N\)维希尔伯特空间有

\[\mathcal{H}\cong \mathbb{C}^N。\]

如果两个向量\(|v\rangle,|w\rangle\) 满足 \(\langle w |v \rangle = 0\), 则我们称这两个向量是正交的。如果我们选定一组基\(\{|i\rangle|i=0,\cdots,N-1\}\), 满足

\[\begin{split}\langle j | i\rangle = \delta_{ij} = \begin{cases} & 1, \quad i = j\\ & 0, \quad i\neq j\\ \end{cases},\end{split}\]

且\(\|i\|_2=1, \forall i\), 那么这组基称为正交归一。如不明确说明，接下来我们都将使用正交归一基。这样\(|\psi\rangle\)就可以表示为:

\[|\psi\rangle = \sum_i \psi_i |i\rangle \cong（\psi_0,\cdots, \psi_{N-1})^T, \quad \psi_i \in \mathbb{C}，\quad \sum_i |\psi_i|^2 = 1。\]

例子：考虑一个二维系统\(\mathcal{H}\cong \mathbb{C}^2\)，定义两个基向量为\(|0\rangle\)和\(|1\rangle\)。这样任意量子态可以表示为

其中\(\alpha,\beta\)都是复数。

在正交归一基下，任意两个向量 \(|u\rangle\)，\(|v\rangle\) 的內积可以简化为：

\[\begin{split}\langle v|w\rangle = (v_0^*, \cdots, v_{N-1}^*)\left( \begin{array}{c} w_0 \\ \vdots \\ w_{N-1}\\ \end{array} \right) = \sum_j v^*_jw_j\end{split}\]

类似地，我们可以定义两个向量之间的外积及其在基\(\{|j\rangle\}\)下的表示：

\[\begin{split}|v\rangle \langle w| \cong \left( \begin{array}{c} v_0 \\ \vdots \\ v_{N-1}\\ \end{array} \right) (w_0^*, \cdots, w_{N-1}^*) = \left( \begin{array}{ccc} v_0w_0^* & \ldots & v_0w_{N-1}^* \\ \vdots & \ddots & \vdots \\ v_{N-1}w^*_0 & \ldots & v_{N-1}w^*_{N-1}\\ \end{array} \right)。\end{split}\]

注意，与內积不同，外积是一个作用在\(\mathcal{H}\)上的算子（矩阵）。

1.2 公设2：薛定谔方程(Schördinger equation)#

系统演化：封闭量子系统的演化由薛定谔方程描述：

\[i \frac{d|\psi(t)\rangle}{dt} = H(t) |\psi(t)\rangle,\]

其中\(t\)是时间，\(H(t)\) 是一个厄米算子，称为系统的哈密顿量。

说明：

这里我们使用了原子单位，即约化普朗克常数\(\hbar = 1\)。
对量子计算来说，我们可能不用太关心\(H(t)\)的具体细节（只需要知道他是一个厄米矩阵)，而更关心信息的载体——量子态的演化。这样，从时间\(t_i\) 到\(t_f\)，由薛定谔方程，系统从\(|\psi(t_i)\rangle\) 演化至 \(|\psi(t_f)\rangle\)可以等效地写为:

\[|\psi(t_f)\rangle = U(t_f, t_i) |\psi(t_i)\rangle，\]

这里\(U(t_f, t_i)\)是一个幺正算符（矩阵），具体推导可见Nielson and Chuang教科书第二章。

原则上只要我们知道一个系统的哈密顿量，那么我们就可以完全了解系统的动力学。确定具体的哈密顿量就是在量子力学框架下理论物理的研究目标——不同的的物理系统会涉及到不同的哈密顿量，但这不是量子力学作为基本框架所关心的问题。
在量子计算中，量子逻辑门正是一种幺正变换，其实现是靠工程上构建不同的哈密顿量来产生。详细的细节见第三章。

1.3 公设3: 量子态测量 (state measurement)#

量子态测量（Born 法则）：量子测量是由一组\(\{M_k\}_{k=1}^l\)的测量算子组成，这组算子满足 \(\sum_k M_k^\dagger M_k = I\)。对任意量子态\(|\psi\rangle\in \mathcal{H}\),在测量之后立刻以概率\(p_k\)变成

\[|\psi\rangle\mapsto \frac{M_k|\psi\rangle}{\sqrt{p_k}} = |\psi_k\rangle\]

说明：

\(M^\dagger\) 代表\(M\)的共轭转置，即\(M^\dagger_{ij} = M^*_{ji}\)。
测量结果为指标\(k\)，同时量子态发生了“塌缩”, \(|\psi\rangle\) “瞬间”变成了\(|\psi_k\rangle\)。我们可以验证

\[\sum_k p_k = \langle \psi | \sum_k M_k^\dagger M_k |\psi \rangle = 1。\]

冯-诺依曼（von Neumann）测量。在实际中，我们需要对一实际物理量进行测量（例如坐标，动量，角动量、能量等）。这些物理量在量子力学中都是厄米算子。原则上，在有限维\(\mathcal{H}\)上, 我们可以对任意厄米算子\(O\)进行测量。任意厄米算子\(O\) 可以进行如下分解

\[O = \sum_j \lambda_j |j\rangle\langle j|,\]

其中，\(\{|j\rangle\}\)是一组正交归一基，称为\(O\)的本征向量（eigenstate）,\(\lambda_j\) 称为 \(|j\rangle\)对应的本征值（eigenvalue）。对\(O\)进行测量，即设定

\[M_k=P_k= |k \rangle\langle k |,\]

那么我们测量到\(k\) 的概率为 \(p_k=\langle\psi|P_k|\psi\rangle\), 对应测到的物理量的值为\(\lambda_k\)。

例：假设\(|\psi\rangle = \alpha|0\rangle + \beta|1\rangle\)，我们需要测量厄米算子

\[\begin{split}Z=\left( \begin{array}{cc} 1 & 0 \\ 0 & -1 \\ \end{array} \right)\end{split}\]

\[\begin{split}X=\left( \begin{array}{cc} 0 & 1 \\ 1 & 0 \\ \end{array} \right)\end{split}\]

注意\(X\)的本征是为\(1\)和\(-1\)，对应的本征向量为\(|+\rangle=\frac{1}{\sqrt{2}}(|0\rangle+|1\rangle)\)和\(|-\rangle=\frac{1}{\sqrt{2}}(|0\rangle-|1\rangle)\) (注意 \(\langle-|+\rangle=0\) )。那么我们可以将量子态表示为

\[\begin{split}\begin{aligned} |\psi\rangle &= \alpha|0\rangle + \beta|1\rangle = \frac{\alpha}{\sqrt{2}}(|+\rangle+|-\rangle) + \frac{\beta}{\sqrt{2}}(|+\rangle-|-\rangle)\\ &=\frac{\alpha+\beta}{\sqrt{2}}|+\rangle + \frac{\alpha-\beta}{\sqrt{2}}|-\rangle \end{aligned}\end{split}\]

公设3作为一条公设的基础地位非常具有争议性。如果将测量设备看成是量子力学系统，被测量的量子系统和测量设备一起形成一个更大的、孤立的、量子力学系统。根据公设2，这个更大的孤立系统的演化可以用单一幺正变换来描述。是否有可能根据这种观点推导出公设3？即测量结果的随机性能否从确定的薛定谔方程推导出来？尽管沿着这些方向进行了大量研究，但仍然面临极大的困难，有些甚至是根本性的。这里，我们将采取非常务实的方法，即在实践中很清楚何时应用公设2（只涉及微观系统），何时使用公设3（宏观的仪器参与测量的过程）。这样，我们就必须明确一条宏观和微观的界限。

1.4 公设4：多体量子系统#

给定两个具有各自希尔伯特空间的量子系统\(\mathcal{H}_1\)和\(\mathcal{H}_2\) 那么他们组合量子系统对应的希尔伯特空间是这两个空间的直积：\(\mathcal{H}_1\otimes \mathcal{H}_2\) .

说明：

这里两个希尔伯特空间可以代表完全不同的物理系统。例如：第一个系统可以是电子自旋，而第二系统可以是光子的极化。
关于直积：定义\(\mathcal{H}_1 = \text{span}\{|v_i\rangle\}_{i=0}^{d_1-1}\), \(\mathcal{H}_2 = \text{span}\{|w_i\rangle\}_{i=0}^{d_2-1}\)，那么\(\mathcal{H} = \text{span}\{|v_i\rangle\otimes |w_j\rangle\}_{i=0,j=0}^{d_1-1,d_2-1}\) 。考虑两个量子态\(|\psi\rangle\in\mathcal{H}_1\), \(|\varphi\rangle\in \mathcal{H}_2\), 那么他们的直积是

\[|\psi\rangle\otimes |\varphi\rangle = (\psi_0, \cdots, \psi_{d_1-1})^T \otimes (\varphi_0, \cdots, \varphi_{d_2-1})^T = (\psi_0\varphi_0\cdots, \psi_0\varphi_{d_2-1},\cdots,\psi_{d_1-1}\varphi_{d_2-1})^T.\]

我们也可以定义矩阵的直积：如果

\[\begin{split}A = \left( \begin{array}{ccc} a_{0,0} & \ldots & a_{0,d_1-1} \\ \vdots & \ddots & \vdots \\ a_{d_1-1,0} & \ldots & a_{d_1-1,d_1-1}\\ \end{array} \right), \quad B = \left( \begin{array}{ccc} b_{0,0} & \ldots & b_{0,d_2-1} \\ \vdots & \ddots & \vdots \\ b_{d_2-1,0} & \ldots & b_{d_2-1,d_2-1}\\ \end{array} \right), \quad\end{split}\]

那么

\[\begin{split}A\otimes B = \left( \begin{array}{ccc} a_{0,0}B & \ldots & a_{0,d_1-1}B \\ \vdots & \ddots & \vdots \\ a_{d_1-1,0}B & \ldots & a_{d_1-1,d_1-1}B\\ \end{array} \right).\end{split}\]

更多的量子系统的可以通过类似地方式构造其希尔伯特空间：考虑\(n\)个系统，那么系统的希尔伯特空间是\(\mathcal{H}=\mathcal{H}_1\otimes \mathcal{H}_2\cdots\otimes \mathcal{H}_n\)。如果第\(k\)个系统的空间维数是\(d_k\),那么整个系统的维数是\(N=\Pi_{k=1}^n d_k\)，需要同样数量的复数来描述。随着\(n\)的增加，复杂性是呈指数上升，这正是量子系统难以计算的原因，也是量子计算潜在计算能力的来源。

例子：考虑一个二维系统和一个三维系统，那么\(\mathcal{H}=\mathcal{H}_1\otimes \mathcal{H}_2=\mathbb{C}^{2}\otimes \mathbb{C}^3\cong \mathbb{C}^{6}\)。如果\(|\psi\rangle = \alpha|0\rangle+\beta|1\rangle\in \mathcal{H}_1\)， \(|\phi\rangle=\gamma|0\rangle+\delta|1\rangle + \xi |2\rangle\in \mathcal{H}_2\)，那么

1.5 量子概率与经典概率#

现在，我们已经了解了量子力学的全部原理。我们可以发现，量子力学的原理与牛顿力学和麦克斯韦方程描述的电磁学（两者统称为经典物理学）完全不同，体现在根本没有“力”这个概念。事实上，由于量子力学的几率本质，他与经典概率学的关系更为密切，而“力”的性质体现在决定系统演化的哈密顿量之中。考虑一个包含 \(n\) 个可能取值的随机变量，我们可以定义其几率分布：

\[\vec{p} = (p_1,p_2, \cdots, p_N)^T, \quad p_i \in \mathbb{R}_+, \sum_i {p_i} = 1。\]

经过一个经典信息处理过程后，概率分布发生了变化，我们可以用一个线性变换描述这个过程：

\[\vec{p}' = \mathcal{T} \vec{p},\]

这里矩阵\(T\)定义为：

\[\begin{split}\mathcal{T} = \left( \begin{array}{cccc} p(1|1) & p(1|2) & \ldots & p(1|N) \\ p(2|1) & p(2|2) & \ldots & p(N|N) \\ \vdots & \vdots & \ddots & \vdots \\ p(N|1) & p(N|2) & \ldots & p(N|N) \\ \end{array} \right)\end{split}\]

称为概率转移矩阵，其中\(p(i|j)\in \mathbb{R}\)就是条件概率。我们可以简单地验证：\(p'_j = \sum_i p(j|i)p(i)\)。

类似地，在量子力学里，我们也有量子态的几率幅分布：

\[|\psi\rangle = (\psi_0, \psi_1, \cdots, \psi_{N-1})^T, \quad, \psi_i \in \mathbb{C}, \quad \sum_{i} |\psi_i|^2 =1\]

对量子态的信息处理也可以看成是一个变换：

\[|\phi\rangle = U|\psi\rangle= \sum_j \left(\sum_lU_{jl}\psi_l\right)|j\rangle =\sum_j\phi_j |j\rangle,\]

其中

\[\begin{split}U = \left( \begin{array}{cccc} U_{1|1} & U_{1|2} & \ldots & U_{1|N} \\ U_{2|1} & U_{2|2} & \ldots & U_{2|N} \\ \vdots & \vdots & \ddots & \vdots \\ U_{N|1} & U_{N|2} & \ldots & U_{N|N} \\ \end{array} \right).\end{split}\]

这里，我们可以发现量子和经典概率的相似性——\(U\)可以看成是量子概率幅的转移矩阵。我们可以发现，正是由于Born法则的的要求可以验证，为了满足\(\sum_j|\phi_j|^2 = 1\)以保证测量结果的统计解释, \(U\)必须是一个幺正矩阵，这也正呼应了公设2的要求。我们可以对一个向量\(v\)定义\(l_p\)长度:

\[\| v\|_p = \left(\sum_i |v_i|^p\right)^{1/p} , \quad p\in N_+，\]

那么更抽象地说，经典信息处理是对\(\mathbb{R}_+^{n}\) 进行保持\(l_1\)的变换，而量子信息处理是对\(\mathbb{C}^n\)进行保持\(l_2\)的变换（\(N\)维幺正矩阵）。

2. 量子比特（qubit）#

为了利用量子力学的性质进行信息处理，我们需要进行信息编码。量子比特就是这种编码的基本载体。数学上来看，量子比特只是量子系统的一种特殊形式（维数为2的希尔伯特空间）。在本节，我们将利用之前学到的量子力学原理来进一步了解量子比特。

2.1 单量子比特和Bloch球#

简而言之，单个量子比特就是一个二维的希尔伯特空间 \(\cong\mathbb{C}^{2}\) 。我们可以分别定义\(|0\rangle\)和\(|1\rangle\)态来编码信息0和1：

\[\begin{split}|0\rangle = \left( \begin{array}{c} 1 \\ 0 \\ \end{array} \right), \quad |1\rangle = \left( \begin{array}{c} 0 \\ 1 \\ \end{array} \right), \quad\end{split}\]

\(|0\rangle\)和\(|1\rangle\)同时也构成希尔伯特空间的基向量。任意单量子比特态可以表示为：

\[|\psi\rangle = \alpha|0\rangle+\beta|1\rangle = C(\cos(\theta/2)|0\rangle+e^{i\varphi}\sin(\theta/2)|1\rangle) \cong \cos(\theta/2)|0\rangle+e^{i\varphi}\sin(\theta/2)|1\rangle，\]

其中\(C\)作为一个常数没有物理意义。另外\(\theta\in[-\pi, \pi)\), \(\varphi\in[0,2\pi）\)。这样,单个量子比特态仅仅需要2个角度就能完全刻画，而这两个角正好可以对应球坐标中的方位角(\(\theta\))和极角\((\varphi)\)（如下图所示）。这样就赋予了每个量子态独特的几何意义：单个量子比特的量子态对应一个单位球面上的一点，这个球称为Bloch球。我们可以验证，\(|0\rangle\)和\(|1\rangle\)正位于Bloch球的北极和南极。

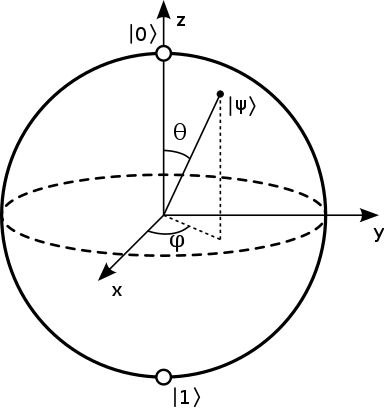
f4a766c874b2494289c4d301e5236ee0

Bloch 球

2.2 多量子比特和量子纠缠（entanglement）#

为了进行信息处理，我们也要考虑使用多个量子比特。考虑 \(n\) 个量子比特，那么根据公设4, 我们需要处理的希尔伯特空间是\(\mathbb{C}^{2^n}\)，这个空间是由以下\(2^n\)个基向量张成：

\[\begin{split}\begin{aligned} \{&|0_10_20_3\cdots0_{n-1}0_n\rangle, |0_10_20_3\cdots0_{n-1}1_n\rangle, |0_10_20_3\cdots1_{n-1}0_n\rangle, \\ &|0_10_20_3\cdots1_{n-1}1_n\rangle, \cdots \cdots， |1_1 1_2 1_3\cdots0_{n-1}0_n\rangle, |1_1 1_2 1_3\cdots0_{n-1}1_n\rangle，\\ &|1_1 1_2 1_3\cdots1_{n-1}0_n\rangle,|1_1 1_2 1_3\cdots 1_{n-1}1_n\rangle\}。 \end{aligned}\end{split}\]

以 \(n=2\) 为例，我们可以有一个最大纠缠态（也称为Bell态）：

\[|\Phi_+\rangle = \frac{1}{\sqrt{2}}(|00\rangle + |11\rangle) = (1/\sqrt{2}, 0, 0, 1/\sqrt{2})^T。\]

这个量子态无法分解成两个量子态的直积（满足这种条件的量子态称为可分离态），具有经典概率不能描述的统计性质，在量子信息学中具有极其重要的意义。同样地，当\(n=3\)时，我们也能找到一类相似的纠缠态：

\[|{\rm GHZ}\rangle = \frac{1}{\sqrt{2}}(|000\rangle + |111\rangle) =(1/\sqrt{2} , 0 , 0 , 0 , 0 , 0 , 0 , 1/\sqrt{2})^T。\]

事实上，与直觉相反，纠缠态无处不在，而可分离态却非常少。纠缠态的性质较为复杂，遗憾的是，对多量子比特系统，哪怕是在 \(n=2\) 的情形下，我们也没有像单个量子比特那样清晰的几何图像帮助我们理解。我们在下一节也会看到，一些特殊的纠缠态正是量子算法可以加速完成计算任务的关键。值得注意的是，多量子比特的纠缠态是非常复杂的。当多个量子比特纠缠在一起时，单个量子比特的量子态信息会在某种意义上变得不确定，所以我们有时需要消除不需要的纠缠。

例子：对纠缠态的测量。如果我们对\(|\Phi_+\rangle\)第一个量子比特进行\(Z\)的测量。那么我们有\(P_0 = |0_0\rangle\langle0_0|, P_1 = |1_0\rangle\langle 1_0|\), 和\(p_0 = 1/2\), \(p_1=1/2\)。在测量结束后，我们以概率\(1/2\)得到\(0\)和\(1\),两比特系统相应的最终态为\(|00\rangle\) 和 \(|11\rangle\)，量子纠缠不再存在。这里我们注意到，当测量第一个量子比特得到结果0时，第二个量子比特也必须同时塌缩到\(|0\rangle\)态。

2.3 密度矩阵#

2.3.1 纯态与混合态#

一个纯态的量子系统，其量子态可以用态向量表示 \(|\psi \rangle\)。而几种纯态依照概率组成的量子态称为混合态。例如，假设一个量子系统处于纯态 \(|\psi _{1}\rangle |\psi _{2}\rangle\) 的概率都为50%，则这量子系统处于混合态。密度矩阵专门用来表示混合态。任何量子态，不管是纯态，还是混合态，都可以用密度矩阵表示。

混合态与叠加态的概念不同，几种纯态通过量子叠加所组成的叠加态仍旧是纯态。例如，\((|\psi _{1}\rangle +|\psi _{2}\rangle )/\sqrt {2}\) 是个纯态。

2.3.2 密度矩阵 (density matrix)#

假设一个量子系统处于纯态 \(|\psi _{1}\rangle、|\psi _{2}\rangle、|\psi _{3}\rangle\)、……的概率分别为 \(w_{1}、w_{2}、w_{3}\)、……，则这混合态量子系统的密度算符 \(\rho\) 为

\[{\rho }=\sum _{i}w_{i}|\psi _{i}\rangle \langle \psi _{i}|\]

注意到所有概率的总和为1：

\[\sum _{i}w_{i}=1\]

第二章 量子力学 (Quantum Mechanics)#